Soalan 1:
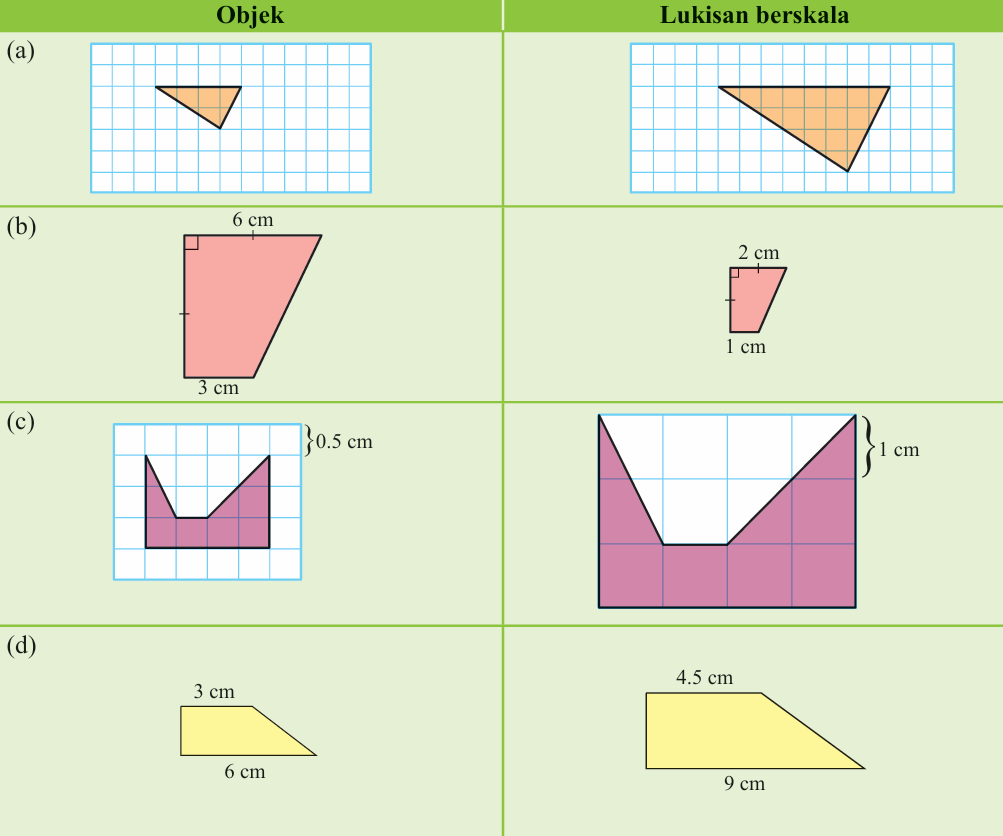
Tentukan skala yang digunakan untuk setiap lukisan berskala di bawah dalam bentuk 1 : n.
Penyelesaian:
1. Lukisan Berskala ialah lukisan suatu objek dengan keadaan semua ukuran dalam lukisan adalah berkadaran dengan ukuran pada objek.
$$ \text { Skala }=\frac{\text { Ukuran lukisan berskala }}{\text { Ukuran objek }}=\frac{1}{n} $$
2. Secara lazimnya, untuk lukisan berskala, kita menggunakan skala dalam bentuk nisbah.
$$ \begin{aligned} &1: n\\ &\text { dengan keadaan } n \text { ialah integer positif atau pecahan } \end{aligned} $$
1 : n bermaksud satu unit pada lukisan berskala akan mewakili n unit pada objek,
Jika n < 1, maka saiz lukisan berskala lebih besar daripada saiz objek
Iika n > 1, maka saiz lukisan berskala lebih kecil daripada saiz objek,
Iika n = 1, maka saiz lukisan berskala sama dengan saiz obiek.
(a)
$$ \begin{aligned} \text { Skala } & =\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} \\ & =\frac{8}{4} \\ & =\frac{2}{1} \end{aligned} $$
$$ \begin{aligned} \text { Skala } & =2: 1 \\ & =\frac{2}{2}: \frac{1}{2} \\ & =1: \frac{1}{2} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Skala } & =\frac{2 \mathrm{~cm}}{6 \mathrm{~cm}} \\ & =\frac{1}{3} \\ & =1: 3 \end{aligned} $$
(c)
$$ \begin{aligned} \text { Skala } & =\frac{\text { Saiz grid lukisan berskala }}{\text { Saiz grid objek }} \\ & =\frac{1 \mathrm{~cm}}{0.5 \mathrm{~cm}} \\ & =\frac{2}{1} \end{aligned} $$
$$ \begin{aligned} \text { Skala } & =2: 1 \\ & =\frac{2}{2}: \frac{1}{2} \\ & =1: \frac{1}{2} \end{aligned} $$
(d)
$$ \begin{aligned} \text { Skala } & =\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} \\ & =\frac{4.5 \mathrm{~cm}}{3 \mathrm{~cm}} \\ & =\frac{3}{2} \end{aligned} $$
$$ \begin{aligned} \text { Skala } & =3: 2 \\ & =\frac{3}{3}: \frac{2}{3} \\ & =1: \frac{2}{3} \end{aligned} $$
Tentukan skala yang digunakan untuk setiap lukisan berskala di bawah dalam bentuk 1 : n.

Penyelesaian:
1. Lukisan Berskala ialah lukisan suatu objek dengan keadaan semua ukuran dalam lukisan adalah berkadaran dengan ukuran pada objek.
$$ \text { Skala }=\frac{\text { Ukuran lukisan berskala }}{\text { Ukuran objek }}=\frac{1}{n} $$
2. Secara lazimnya, untuk lukisan berskala, kita menggunakan skala dalam bentuk nisbah.
$$ \begin{aligned} &1: n\\ &\text { dengan keadaan } n \text { ialah integer positif atau pecahan } \end{aligned} $$
1 : n bermaksud satu unit pada lukisan berskala akan mewakili n unit pada objek,
Jika n < 1, maka saiz lukisan berskala lebih besar daripada saiz objek
Iika n > 1, maka saiz lukisan berskala lebih kecil daripada saiz objek,
Iika n = 1, maka saiz lukisan berskala sama dengan saiz obiek.
(a)
$$ \begin{aligned} \text { Skala } & =\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} \\ & =\frac{8}{4} \\ & =\frac{2}{1} \end{aligned} $$
$$ \begin{aligned} \text { Skala } & =2: 1 \\ & =\frac{2}{2}: \frac{1}{2} \\ & =1: \frac{1}{2} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Skala } & =\frac{2 \mathrm{~cm}}{6 \mathrm{~cm}} \\ & =\frac{1}{3} \\ & =1: 3 \end{aligned} $$
(c)
$$ \begin{aligned} \text { Skala } & =\frac{\text { Saiz grid lukisan berskala }}{\text { Saiz grid objek }} \\ & =\frac{1 \mathrm{~cm}}{0.5 \mathrm{~cm}} \\ & =\frac{2}{1} \end{aligned} $$
$$ \begin{aligned} \text { Skala } & =2: 1 \\ & =\frac{2}{2}: \frac{1}{2} \\ & =1: \frac{1}{2} \end{aligned} $$
(d)
$$ \begin{aligned} \text { Skala } & =\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} \\ & =\frac{4.5 \mathrm{~cm}}{3 \mathrm{~cm}} \\ & =\frac{3}{2} \end{aligned} $$
$$ \begin{aligned} \text { Skala } & =3: 2 \\ & =\frac{3}{3}: \frac{2}{3} \\ & =1: \frac{2}{3} \end{aligned} $$
Soalan 2:
Sekeping poster berukuran 24 cm panjang dan 8 cm lebar. Hitung panjang dan lebar lukisan berskala poster itu, dalam cm, yang dilukis mengikut skala 1 : 4.
Penyelesaian:
$$ \text { Skala }=\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} $$
$$ \begin{aligned} \frac{1}{4} & =\frac{\text { Panjang lukisan berskala }}{24 \mathrm{~cm}} \\ \text { Panjang lukisan berskala } & =\frac{1}{4} \times 24 \mathrm{~cm} \\ & =6 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \frac{1}{4} & =\frac{\text { Lebar lukisan berskala }}{8 \mathrm{~cm}} \\ \text { Lebar lukisan berskala } & =\frac{1}{4} \times 8 \mathrm{~cm} \\ & =2 \mathrm{~cm} \end{aligned} $$
Maka, panjang dan lebar lukisan berskala adalah 6 cm dan 2 cm masing-masing.
Sekeping poster berukuran 24 cm panjang dan 8 cm lebar. Hitung panjang dan lebar lukisan berskala poster itu, dalam cm, yang dilukis mengikut skala 1 : 4.
Penyelesaian:
$$ \text { Skala }=\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} $$
$$ \begin{aligned} \frac{1}{4} & =\frac{\text { Panjang lukisan berskala }}{24 \mathrm{~cm}} \\ \text { Panjang lukisan berskala } & =\frac{1}{4} \times 24 \mathrm{~cm} \\ & =6 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \frac{1}{4} & =\frac{\text { Lebar lukisan berskala }}{8 \mathrm{~cm}} \\ \text { Lebar lukisan berskala } & =\frac{1}{4} \times 8 \mathrm{~cm} \\ & =2 \mathrm{~cm} \end{aligned} $$
Maka, panjang dan lebar lukisan berskala adalah 6 cm dan 2 cm masing-masing.
Soalan 3:
Sebuah peta dilukis dengan skala 1 : 400 000. Berapakah jarak sebenar, dalam km, yang diwakili oleh sebatang sungai yang panjangnya 2.5 cm pada peta tersebut?
Penyelesaian:
$$ \begin{aligned} &\begin{aligned} \text { Skala } & =\frac{\text { Ukuran lukisan berskala }}{\text { Ukuran objek }} \\ \frac{1}{400000} & =\frac{2.5 \mathrm{~cm}}{\text { Jarak sebenar sungai }} \end{aligned}\\ &\begin{aligned} \text { Jarak sebenar sungai } & =2.5 \mathrm{~cm} \times 400 \\ & =1000000 \mathrm{~cm} \\ & =\frac{1000000}{100000} \\ & =10 \mathrm{~km} \end{aligned} \end{aligned} $$
Imbas kembali:
1 km = 1 000 m
1 m = 100 cm
1 km = 100 000 cm
Sebuah peta dilukis dengan skala 1 : 400 000. Berapakah jarak sebenar, dalam km, yang diwakili oleh sebatang sungai yang panjangnya 2.5 cm pada peta tersebut?
Penyelesaian:
$$ \begin{aligned} &\begin{aligned} \text { Skala } & =\frac{\text { Ukuran lukisan berskala }}{\text { Ukuran objek }} \\ \frac{1}{400000} & =\frac{2.5 \mathrm{~cm}}{\text { Jarak sebenar sungai }} \end{aligned}\\ &\begin{aligned} \text { Jarak sebenar sungai } & =2.5 \mathrm{~cm} \times 400 \\ & =1000000 \mathrm{~cm} \\ & =\frac{1000000}{100000} \\ & =10 \mathrm{~km} \end{aligned} \end{aligned} $$
Imbas kembali:
1 km = 1 000 m
1 m = 100 cm
1 km = 100 000 cm
Soalan 4:
Siew Lin melukis segi tiga bersudut tegak dengan skala 1 : 1/3. Jika panjang hipotenus 3 lukisan berskala ialah 18 cm, hitung panjang hipotenus segi tiga asal.
Penyelesaian:
$$ \begin{aligned} &\begin{aligned} \text { Skala } & =\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} \\ \frac{1}{\frac{1}{3}} & =\frac{18 \mathrm{~cm}}{\text { Panjang hipotenus segi tiga asal }} \end{aligned}\\ &\begin{aligned} \text { Panjang hipotenus segi tiga asal } & =18 \mathrm{~cm} \times \frac{1}{3} \\ & =6 \mathrm{~cm} \end{aligned} \end{aligned} $$
Siew Lin melukis segi tiga bersudut tegak dengan skala 1 : 1/3. Jika panjang hipotenus 3 lukisan berskala ialah 18 cm, hitung panjang hipotenus segi tiga asal.
Penyelesaian:
$$ \begin{aligned} &\begin{aligned} \text { Skala } & =\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} \\ \frac{1}{\frac{1}{3}} & =\frac{18 \mathrm{~cm}}{\text { Panjang hipotenus segi tiga asal }} \end{aligned}\\ &\begin{aligned} \text { Panjang hipotenus segi tiga asal } & =18 \mathrm{~cm} \times \frac{1}{3} \\ & =6 \mathrm{~cm} \end{aligned} \end{aligned} $$