Soalan 1:
Tulis rumus algebra daripada situasi berikut.
(a) A mewakili luas, manakala x mewakili panjang sisi sebuah segi empat sama. Tulis rumus yang menghubungkan A dengan x.
(b) Bayaran sewa sebuah gelanggang sepak takraw ialah RM5 bagi satu jam yang pertama. Bayaran bagi setiap jam yang berikutnya ialah RM3. Tulis rumus yang menghubungkan jumlah bayaran, p dan jam yang disewa, h.
(c) Pecutan, a ialah perbezaan antara laju akhir, v2 dan laju awal, v1 yang dibahagikan dengan masa, t. Tulis hubungan antara a, v2 , v1 dan t.
Penyelesaian:
(a)
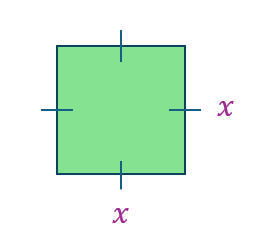
$$ \begin{aligned} &\text { Luas, }\\ &\begin{aligned} & A=(x)(x) \\ & A=x^2 \end{aligned} \end{aligned} $$
(b)
Bayaran sewa untuk 1 jam = RM5
Bayaran sewa untuk 2 jam = RM5 + RM3 = RM8
Bayaran sewa untuk 3 jam = RM5 + RM3 + RM3 = RM11
Maka, rumus yang menghubungkan jumlah bayaran, p dan jam yang disewa, h:
$$ \begin{aligned} & p=5+3(h-1) \\ & p=5+3 h-3 \\ & p=3 h+2 \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Perbezaan antara laju akhir, } v_2 \text { dan laju awal, }\\ &v_1=v_2-v_1 \end{aligned} $$
$$ \begin{aligned} &\text { Kemudian, bahagikan }\left(v_2-v_1\right) \text { dengan } t\\ &\therefore a=\frac{v_2-v_1}{t} \end{aligned} $$
Tulis rumus algebra daripada situasi berikut.
(a) A mewakili luas, manakala x mewakili panjang sisi sebuah segi empat sama. Tulis rumus yang menghubungkan A dengan x.
(b) Bayaran sewa sebuah gelanggang sepak takraw ialah RM5 bagi satu jam yang pertama. Bayaran bagi setiap jam yang berikutnya ialah RM3. Tulis rumus yang menghubungkan jumlah bayaran, p dan jam yang disewa, h.
(c) Pecutan, a ialah perbezaan antara laju akhir, v2 dan laju awal, v1 yang dibahagikan dengan masa, t. Tulis hubungan antara a, v2 , v1 dan t.
Penyelesaian:
(a)

$$ \begin{aligned} &\text { Luas, }\\ &\begin{aligned} & A=(x)(x) \\ & A=x^2 \end{aligned} \end{aligned} $$
(b)
Bayaran sewa untuk 1 jam = RM5
Bayaran sewa untuk 2 jam = RM5 + RM3 = RM8
Bayaran sewa untuk 3 jam = RM5 + RM3 + RM3 = RM11
Maka, rumus yang menghubungkan jumlah bayaran, p dan jam yang disewa, h:
$$ \begin{aligned} & p=5+3(h-1) \\ & p=5+3 h-3 \\ & p=3 h+2 \end{aligned} $$
Bukti : Bagi kegunaan 1 jam, p = 3(1) + 2 = RM5
Bagi kegunaan 2 jam, p = 3(2) + 2 = RM8
Bagi kegunaan 3 jam, p = 3(3) + 2 = RM11
(c)
$$ \begin{aligned} &\text { Perbezaan antara laju akhir, } v_2 \text { dan laju awal, }\\ &v_1=v_2-v_1 \end{aligned} $$
$$ \begin{aligned} &\text { Kemudian, bahagikan }\left(v_2-v_1\right) \text { dengan } t\\ &\therefore a=\frac{v_2-v_1}{t} \end{aligned} $$
Soalan 2:
Ungkapkan huruf dalam kurungan sebagai perkara rumus.
(a) m = –3q + p [q]
(b) x = –p – w [w]
(c) 2e = 4g + 3h [g]
(d) ¾m – 6p = ¾ q [q]
(e) w = 3v2 [v]
(f) 2m = ¾ n2 [n]
$$ \text { (g) } 3 w=\frac{(v+1)^{\frac{1}{2}}}{2} $$
$$ \text { (h) } \frac{5}{4} f=\frac{5}{\sqrt{k-7}} $$
Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} m & =-3 q+p \\ 3 q & =p-m \\ q & =\frac{p-m}{3} \end{aligned}\\ &\text { atau }\\ &\begin{aligned} -3 q+p & =m \\ -3 q & =m-p \\ q & =\frac{m-p}{-3} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} & x=-p-w \\ & w=-p-x \end{aligned} $$
(c)
$$ \begin{array}{rlr} 2 e & =4 g+3 h & \\ -4 g & =3 h-2 e & \quad \text { Kedua-dua belah } \\ 4 g & =2 e-3 h & \text { persamaan didarabkan }(-) \\ g & =\frac{2 e-3 h}{4} & \end{array} $$
(d)
$$ \begin{aligned} \frac{3}{4} m-6 p & =\frac{3}{4} q \\ 3 m-24 p & =3 q \quad \text { Kedua-dua belah persamaan }(\times 4) \\ 3 q & =3 m-24 p \\ q & =m-8 p \longleftarrow \text { Kedua-dua belahpersamaan }(\div 3) \end{aligned} $$
(e)
$$ \begin{aligned} w & =3 v^2 \\ 3 v^2 & =w \\ v^2 & =\frac{w}{3} \\ v & =\sqrt{\frac{w}{3}} \end{aligned} $$
(f)
$$ \begin{aligned} 2 m & =\frac{3}{4} n^2 \\ (2 m)(4) & =3 n^2 \\ 8 m & =3 n^2 \\ 3 n^2 & =8 m \\ n^2 & =\frac{8 m}{3} \\ n & =\sqrt{\frac{8 m}{3}} \end{aligned} $$
(g)
$$ \begin{aligned} 3 w & =\frac{(v+1)^{\frac{1}{2}}}{2} \\ 6 w & =(v+1)^{\frac{1}{2}} \\ (v+1)^{\frac{1}{2}} & =6 w \\ v+1 & =(6 w)^2 \quad \text { Kedua-dua belah persamaan dikuasaduakan } \\ v & =36 w^2-1 \end{aligned} $$
(h)
$$ \begin{aligned} \frac{5}{4} f & =\frac{5}{\sqrt{k-7}} \\ 5 f \times \sqrt{k-7} & =5 \times 4 \\ \sqrt{k-7} & =\frac{20}{5 f} \\ k-7 & =\left(\frac{4}{f}\right)^2 \quad \text { Kedua-dua belah Persamaan dikuasaduakan } \\ k & =\frac{16}{f^2}+7 \end{aligned} $$
Ungkapkan huruf dalam kurungan sebagai perkara rumus.
(a) m = –3q + p [q]
(b) x = –p – w [w]
(c) 2e = 4g + 3h [g]
(d) ¾m – 6p = ¾ q [q]
(e) w = 3v2 [v]
(f) 2m = ¾ n2 [n]
$$ \text { (g) } 3 w=\frac{(v+1)^{\frac{1}{2}}}{2} $$
$$ \text { (h) } \frac{5}{4} f=\frac{5}{\sqrt{k-7}} $$
Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} m & =-3 q+p \\ 3 q & =p-m \\ q & =\frac{p-m}{3} \end{aligned}\\ &\text { atau }\\ &\begin{aligned} -3 q+p & =m \\ -3 q & =m-p \\ q & =\frac{m-p}{-3} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} & x=-p-w \\ & w=-p-x \end{aligned} $$
(c)
$$ \begin{array}{rlr} 2 e & =4 g+3 h & \\ -4 g & =3 h-2 e & \quad \text { Kedua-dua belah } \\ 4 g & =2 e-3 h & \text { persamaan didarabkan }(-) \\ g & =\frac{2 e-3 h}{4} & \end{array} $$
(d)
$$ \begin{aligned} \frac{3}{4} m-6 p & =\frac{3}{4} q \\ 3 m-24 p & =3 q \quad \text { Kedua-dua belah persamaan }(\times 4) \\ 3 q & =3 m-24 p \\ q & =m-8 p \longleftarrow \text { Kedua-dua belahpersamaan }(\div 3) \end{aligned} $$
(e)
$$ \begin{aligned} w & =3 v^2 \\ 3 v^2 & =w \\ v^2 & =\frac{w}{3} \\ v & =\sqrt{\frac{w}{3}} \end{aligned} $$
(f)
$$ \begin{aligned} 2 m & =\frac{3}{4} n^2 \\ (2 m)(4) & =3 n^2 \\ 8 m & =3 n^2 \\ 3 n^2 & =8 m \\ n^2 & =\frac{8 m}{3} \\ n & =\sqrt{\frac{8 m}{3}} \end{aligned} $$
(g)
$$ \begin{aligned} 3 w & =\frac{(v+1)^{\frac{1}{2}}}{2} \\ 6 w & =(v+1)^{\frac{1}{2}} \\ (v+1)^{\frac{1}{2}} & =6 w \\ v+1 & =(6 w)^2 \quad \text { Kedua-dua belah persamaan dikuasaduakan } \\ v & =36 w^2-1 \end{aligned} $$
(h)
$$ \begin{aligned} \frac{5}{4} f & =\frac{5}{\sqrt{k-7}} \\ 5 f \times \sqrt{k-7} & =5 \times 4 \\ \sqrt{k-7} & =\frac{20}{5 f} \\ k-7 & =\left(\frac{4}{f}\right)^2 \quad \text { Kedua-dua belah Persamaan dikuasaduakan } \\ k & =\frac{16}{f^2}+7 \end{aligned} $$