Soalan 7:
Dalam rajah di bawah, AEC dan BCD ialah garis lurus. E ialah titik tengah AC.
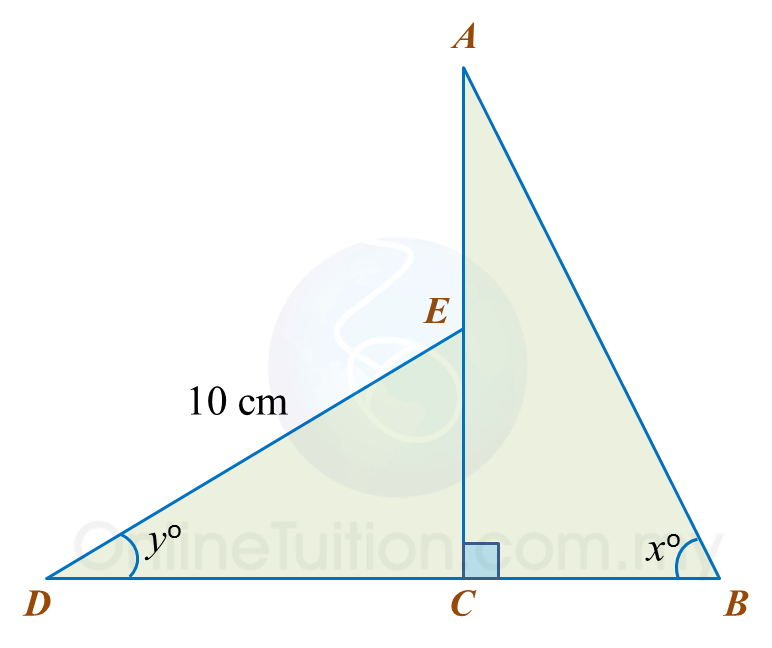
(a) cari nilai tan x.
(b) Hitung panjang, dalam cm, BD.
Penyelesaian:
Dalam rajah di bawah, AEC dan BCD ialah garis lurus. E ialah titik tengah AC.

(a) cari nilai tan x.
(b) Hitung panjang, dalam cm, BD.
Penyelesaian:
Soalan 8:
Dalam rajah di bawah, T ialah titik tengah garis PR.

(a) Cari nilai tan xo.
(b) Hitung panjang, dalam cm, PQ.
Penyelesaian:
Dalam rajah di bawah, T ialah titik tengah garis PR.

(a) Cari nilai tan xo.
(b) Hitung panjang, dalam cm, PQ.
Penyelesaian: