8.2.1 Koordinat, Praktis Berformat PT3
Soalan 1:
Dalam rajah di bawah, Q ialah titik tengah garis lurus PR.
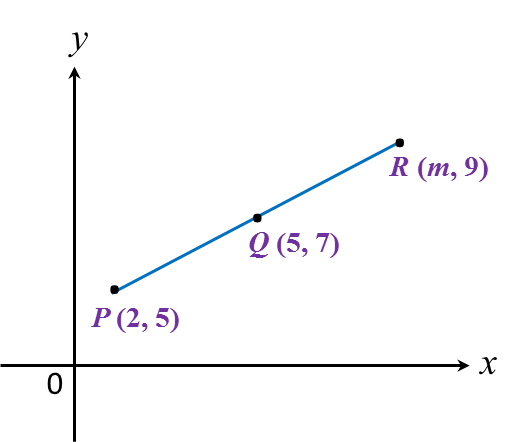
Nilai m ialah
Penyelesaian:
Soalan 2:
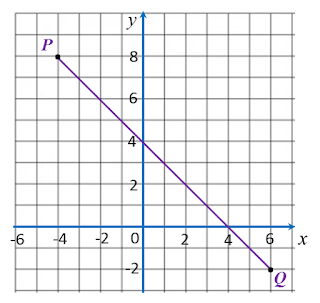
Dalam rajah di bawah, titik P dan titik Q terletak pada suatu satah Cartesan.
Jika M ialah titik tengah PQ, maka koordinat M ialah
Penyelesaian:
Soalan 3:
Cari jarak antara P (–4, 6) dan Q (20, –1).
Penyelesaian: