13.2.1 Teorem Pythagoras, Praktis Berformat PT3
Soalan 1:
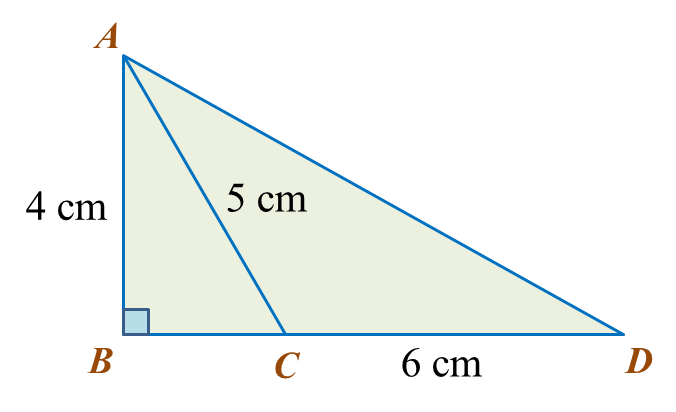

Dalam rajah, ABC ialah segi tiga bersudut tegak dan BCD ialah garis lurus.
Hitungkan panjang AD, betul kepada dua titik perpuluhan.
Hitungkan panjang AD, betul kepada dua titik perpuluhan.
Penyelesaian:
Dalam ∆ ABC,
BC2 = 52 – 42
= 25 – 16
= 9
BC = √9
= 3 cm
Dalam ∆ ABD,
BD = BC + CD
= 3 + 6
= 9
AD2 = 42 + 92
= 16 + 81
= 97
AD = √97
= 9.849
= 9.85 cm
Soalan 2:
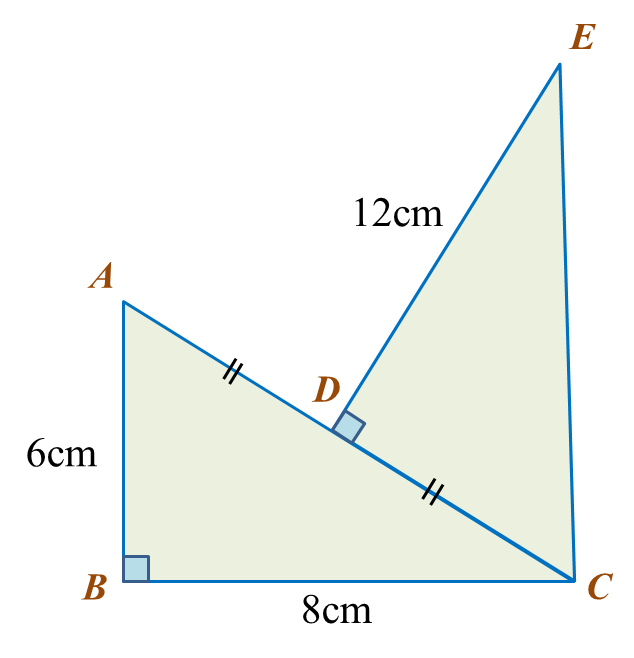

Rajah di atas menunjukkan dua buah segi tiga bersudut tegak.
Hitungkan perimeter seluruh rajah.
Penyelesaian:
Dalam ∆ ABC,
AC2 = 62 + 82
= 36 + 64
= 100
AC = √100
= 10 cm
AD = 5 cm
Dalam ∆ EDC,
EC2 = 122 + 52
= 144 + 25
= 169
EC = √169
= 13 cm
Perimeter seluruh rajah
= AB + BC + CE + DE + AD
= 6 + 8 + 13 + 12 + 5
= 44 cm
Assalamualaikum, minta izin untuk menggunakan bahan ini.
Salam , boleh tahu kenapa utk soalan 2 . Ukuran perimeter tidak termasuk AD , Bukankah perimeter keseluruhan rajah?
Ya, AD memang termasuk dalam ukuran perimeter.