1.3 Nombor Nisbah
1. BODMAS → (Brackets of Division, Multiplication, Addition and Subtraction)
|
Contoh 1:
Penyelesaian:
(a)
–52 ÷ 13 – 15 × 4
= (–52 ÷ 13) – (15 × 4) ← (hitung dari kiri ke kanan; ÷ dan × dimulakan dahulu)
= –4 – 60
= –64
(b)
63 ÷ (16 – 7) × (–2)
= 63 ÷ 9 × (–2) ← (kurungan dimulakan dahulu, kemudian hitung dari kiri ke kanan)
= 7 × (–2)
= –14
(c)
–30 + 9 × 7 – 16
= –30 + (9 × 7) – 16 ← (darabkan dahulu)
= –30 + 63 – 16
= 17
1.3.1 Pecahan Positif dan Negatif
1. Pecahan positif ialah pecahan dengan atau tanpa tanda positif (+) dan mempunyai nilai lebih daripada 0.
2. Pecahan negatif ialah pecahan dengan tanda negatif (–) dan mempunyai nilai kurang daripada 0.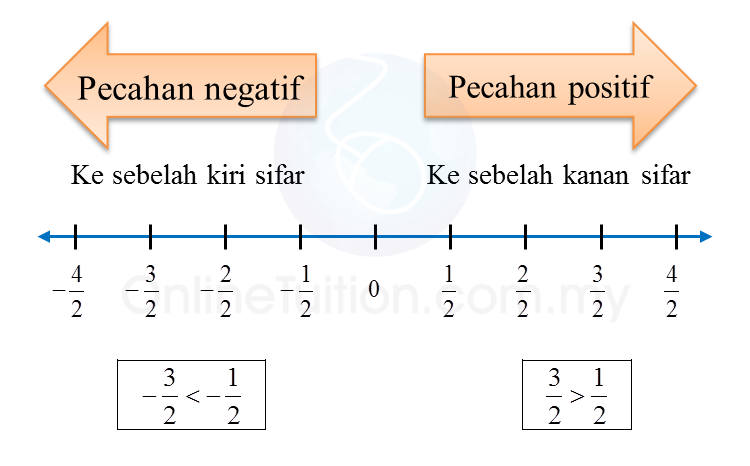
1.3.2 Nombor Perpuluhan Positif dan Negatif
1. Nombor perpuluhan terdiri daripada nombor perpuluhan positif dan nombor perpuluhan negatif.
2. Nombor perpuluhan boleh ditandakan pada suatu garis nombor. Nombor perpuluhan positif terletak di sebelah kanan sifar manakala nombor perpuluhan negatif terletak di sebelah kiri sifar.
1.3.3 Nombor Nisbah
1. Semua Integer ialah nombor nisbah.
2. Peraturan melakukan gabungan operasi +, –, ×, ÷ dan tanda kurung ke atas nombor berarah adalah sama dengan peraturan operasi gabungan ke atas integer.
Contoh 2:
Penyelesaian:
(a)
(b)
[(–28) – (–4)] ÷ (–5.147 – 0.853)
= [–28 + 4] ÷ (–6)
= (–24) ÷ (–6)
= 4
its really help me to do my maths revision
Tq so much :*
You are welcome 🙂