Soalan 4:
Sebuah kotak mengandungi 3 biji bola yang bertanda tiga huruf vokal a, e dan i. Sebiji bola diambil secara rawak dari kotak tersebut dan huruf yang diperoleh dicatatkan. Bola tersebut diletakkan kembali ke dalam kotak dan bola kedua diambil secara rawak dari kotak tersebut.
Dengan bantuan gambar rajah pokok,
Penyelesaian:
(a)
$$
\begin{aligned}
&\text { Ruang sampel, } S\\
&=\{(a, a),(a, e),(a, i),(e, a),(e, e),(e, i),(i, a),(i, e),(i, i)\}
\end{aligned}
$$
(b)
$$
\begin{aligned}
\text { Peristiwa pelengkap huruf lain } & =\text { Peristiwa huruf sama } \\
& =\{(\mathrm{a}, \mathrm{a}),(\mathrm{e}, \mathrm{e}),(\mathrm{i}, \mathrm{i})\}
\end{aligned}
$$
(c)
$$
\begin{aligned}
&\text { Bilangan pelengkap bagi (b) }=9-3=6\\
&\begin{aligned}
P(b)^{\prime} & =\frac{6}{9} \\
& =\frac{2}{3}
\end{aligned}
\end{aligned}
$$
Sebuah kotak mengandungi 3 biji bola yang bertanda tiga huruf vokal a, e dan i. Sebiji bola diambil secara rawak dari kotak tersebut dan huruf yang diperoleh dicatatkan. Bola tersebut diletakkan kembali ke dalam kotak dan bola kedua diambil secara rawak dari kotak tersebut.
Dengan bantuan gambar rajah pokok,
(a) senaraikan ruang sampel bagi eksperimen tersebut.
(b) senaraikan semua unsur peristiwa pelengkap memperoleh huruf yang berlainan.
(c) hitung kebarangkalian peristiwa pelengkap bagi (b)
Penyelesaian:

(a)
$$
\begin{aligned}
&\text { Ruang sampel, } S\\
&=\{(a, a),(a, e),(a, i),(e, a),(e, e),(e, i),(i, a),(i, e),(i, i)\}
\end{aligned}
$$
(b)
$$
\begin{aligned}
\text { Peristiwa pelengkap huruf lain } & =\text { Peristiwa huruf sama } \\
& =\{(\mathrm{a}, \mathrm{a}),(\mathrm{e}, \mathrm{e}),(\mathrm{i}, \mathrm{i})\}
\end{aligned}
$$
(c)
$$
\begin{aligned}
&\text { Bilangan pelengkap bagi (b) }=9-3=6\\
&\begin{aligned}
P(b)^{\prime} & =\frac{6}{9} \\
& =\frac{2}{3}
\end{aligned}
\end{aligned}
$$
Soalan 5:
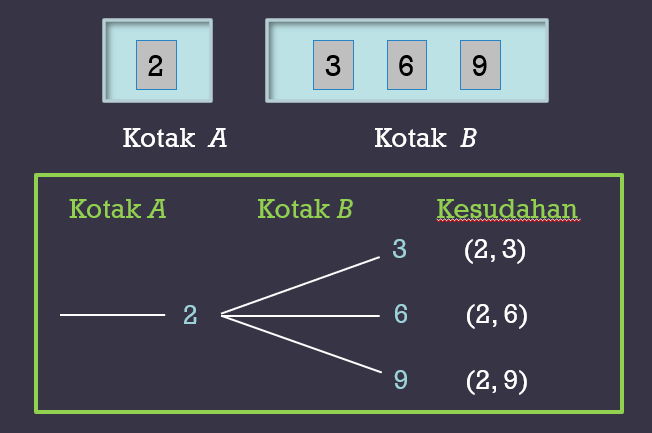
Kotak A diisi dengan sekeping kad sebutan pertama gandaan 2 dan kotak B diisi dengan tiga keping kad, tiga sebutan pertama gandaan 3. Satu kad diambil secara rawak dari kotak A dan B. Dengan bantuan gambar rajah pokok, senaraikan semua unsur dalam ruang sampel bagi eksperimen ini dan hitung kebarangkalian peristiwa mendapat
Penyelesaian:
$$
\text { Ruang sampel, } S=\{(2,3),(2,6),(2,9)\}
$$
(a)
$$
\begin{aligned}
& \text { Peristiwa Gandaan dua } \\
& \qquad \begin{aligned}
P(G 2) & =\frac{n(G 2),(2,6),(2,9)\}}{n(S)} \\
& =\frac{3}{3}=1
\end{aligned}
\end{aligned}
$$
(b)
$$
\begin{aligned}
& \text { Peristiwa Gandaan tiga }=\{(2,3),(2,6),(2,9)\} \\
& \qquad \begin{aligned}
P(G 3) & =\frac{n(G 3)}{n(S)} \\
& =\frac{3}{3}=1
\end{aligned}
\end{aligned}
$$
(c)
$$
\begin{aligned}
& \text { Peristiwa nombor ganjil }=\{(2,3),(2,9)\} \\
& \qquad \begin{aligned}
P(N G) & =\frac{n(N G)}{n(S)} \\
& =\frac{2}{3}
\end{aligned}
\end{aligned}
$$
Kotak A diisi dengan sekeping kad sebutan pertama gandaan 2 dan kotak B diisi dengan tiga keping kad, tiga sebutan pertama gandaan 3. Satu kad diambil secara rawak dari kotak A dan B. Dengan bantuan gambar rajah pokok, senaraikan semua unsur dalam ruang sampel bagi eksperimen ini dan hitung kebarangkalian peristiwa mendapat
(a) sekurang-kurangnya satu nombor gandaan dua dipilih.
(b) sekurang-kurangnya satu nombor gandaan tiga dipilih.
(c) satu nombor ganjil.
Penyelesaian:
$$
\text { Ruang sampel, } S=\{(2,3),(2,6),(2,9)\}
$$
(a)
$$
\begin{aligned}
& \text { Peristiwa Gandaan dua } \\
& \qquad \begin{aligned}
P(G 2) & =\frac{n(G 2),(2,6),(2,9)\}}{n(S)} \\
& =\frac{3}{3}=1
\end{aligned}
\end{aligned}
$$
(b)
$$
\begin{aligned}
& \text { Peristiwa Gandaan tiga }=\{(2,3),(2,6),(2,9)\} \\
& \qquad \begin{aligned}
P(G 3) & =\frac{n(G 3)}{n(S)} \\
& =\frac{3}{3}=1
\end{aligned}
\end{aligned}
$$
(c)
$$
\begin{aligned}
& \text { Peristiwa nombor ganjil }=\{(2,3),(2,9)\} \\
& \qquad \begin{aligned}
P(N G) & =\frac{n(N G)}{n(S)} \\
& =\frac{2}{3}
\end{aligned}
\end{aligned}
$$
Soalan 6:
Hazrin mempunyai hobi mengumpul setem. Dia mempunyai sejumlah 75 keping setem dari negara Indonesia, Singapura, Thailand, Filipina dan Malaysia. Sekeping setem diambil secara rawak. Kebarangkalian mendapat setem dari Thailand dan Filipina ialah 3/5. Jika jumlah setem dari Singapura dan Indonesia menyamai jumlah setem dari Malaysia, hitung kebarangkalian mendapat setem dari Malaysia.
Hazrin mempunyai hobi mengumpul setem. Dia mempunyai sejumlah 75 keping setem dari negara Indonesia, Singapura, Thailand, Filipina dan Malaysia. Sekeping setem diambil secara rawak. Kebarangkalian mendapat setem dari Thailand dan Filipina ialah 3/5. Jika jumlah setem dari Singapura dan Indonesia menyamai jumlah setem dari Malaysia, hitung kebarangkalian mendapat setem dari Malaysia.
Penyelesaian:
$$
\begin{aligned}
& \mathrm{P}(T+F)=\frac{3}{5} \\
& \mathrm{P}(S+I+M)=\frac{2}{5} \\
& \text { Peristiwa }(S+I)=\text { Peristiwa }(M) \\
& \mathrm{P}(M)=\frac{2}{5} \div 2 \\
& \quad=\frac{1}{5}
\end{aligned}
$$