Soalan 3:
Hitung nilai-nilai x yang mungkin bagi setiap persamaan berikut.
$$ \text { (a) } a^{x^2} \div a^{5 x}=\mathrm{a}^6 $$
$$ \text { (b) } 2^{x^2} \times 2^{6 x}=2^7 $$
$$ \text { (c) } 5^{x^2} \div 5^{3 x}=625 $$
Penyelesaian:
(a)
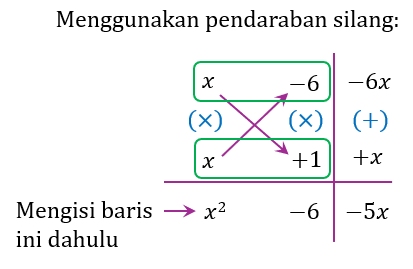
$$ \begin{aligned} a^{x^2} \div a^{5 x} & =a^6 \\ a^{x^2-5 x} & =a^6 \\ x^2-5 x & =6 \\ x^2-5 x-6 & =0 \\ (x-6)(x+1) & =0 \\ x=6 \text { atau } x & =-1 \end{aligned} $$
(b)
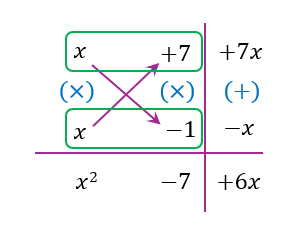
$$ \begin{aligned} 2^{x^2} \times 2^{6 x} & =2^7 \\ 2^{x^2+6 x} & =2^7 \\ x^2+6 x & =7 \\ x^2+6 x-7 & =0 \\ (x+7)(x-1) & =0 \\ x=-7 \text { atau } x & =1 \end{aligned} $$
(c)
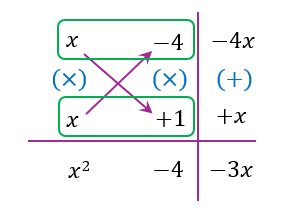
$$ \begin{aligned} 5^{x^2} \div 5^{3 x} & =625 \\ 5^{x^2-3 x} & =5^4 \\ x^2-3 x & =4 \\ x^2-3 x-4 & =0 \\ (x-4)(x+1) & =0 \\ x=4 \text { atau } x & =-1 \end{aligned} $$
Hitung nilai-nilai x yang mungkin bagi setiap persamaan berikut.
$$ \text { (a) } a^{x^2} \div a^{5 x}=\mathrm{a}^6 $$
$$ \text { (b) } 2^{x^2} \times 2^{6 x}=2^7 $$
$$ \text { (c) } 5^{x^2} \div 5^{3 x}=625 $$
Penyelesaian:
(a)
$$ \begin{aligned} a^{x^2} \div a^{5 x} & =a^6 \\ a^{x^2-5 x} & =a^6 \\ x^2-5 x & =6 \\ x^2-5 x-6 & =0 \\ (x-6)(x+1) & =0 \\ x=6 \text { atau } x & =-1 \end{aligned} $$

(b)
$$ \begin{aligned} 2^{x^2} \times 2^{6 x} & =2^7 \\ 2^{x^2+6 x} & =2^7 \\ x^2+6 x & =7 \\ x^2+6 x-7 & =0 \\ (x+7)(x-1) & =0 \\ x=-7 \text { atau } x & =1 \end{aligned} $$

(c)
$$ \begin{aligned} 5^{x^2} \div 5^{3 x} & =625 \\ 5^{x^2-3 x} & =5^4 \\ x^2-3 x & =4 \\ x^2-3 x-4 & =0 \\ (x-4)(x+1) & =0 \\ x=4 \text { atau } x & =-1 \end{aligned} $$

Soalan 4:
Selesaikan persamaan serentak berikut.
$$ \text { (a) } 81^{(x+1)} \times 9^x=3^5 \operatorname{dan} 8^{2 x} \times 4\left(2^{2 y}\right)=128 $$
$$ \text { (b) } 4\left(4^x\right)=8^{y+2} \text { dan } 9^x \times 27^y=1 $$
Penyelesaian:
(a)
$$ \begin{aligned} 81^{(x+1)} \times 9^x & =3^5 \\ 3^{4(x+1)} \times 3^{2 x} & =3^5 \\ 3^{4 x+4} \times 3^{2 x} & =3^5 \\ 3^{4 x+2 x+4} & =3^5 \\ 6 x+4 & =5 \\ 6 x & =5-4 \\ 6 x & =1 \\ x & =\frac{1}{6} …(1) \end{aligned} $$
$$ \begin{aligned} 8^{2 x} \times 4\left(2^{2 y}\right) & =128 \\ \left(2^3\right)^{2 x} \times\left(2^2\right)\left(2^{2 y}\right) & =2^7 \\ 2^{6 x} \times 2^{2+2 y} & =2^7 \\ 2^{6 x+2+2 y} & =2^7 \\ 6 x+2+2 y & =7 \\ 6 x+2 y & =5 …(2) \end{aligned} $$
$$ \begin{aligned} &\text { Gantikan (1) ke dalam (2), }\\ &\begin{aligned} 6\left(\frac{1}{6}\right)+2 y & =5 \\ 1+2 y & =5 \\ 2 y & =5-1 \\ 2 y & =4 \\ y & =\frac{4}{2} \\ y & =2 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} 4\left(4^x\right) & =8^{y+2} \\ 2^2\left(2^{2 x}\right) & =2^{3(y+2)} \\ 2^{2+2 x} & =2^{3 y+6} \\ 2+2 x & =3 y+6 \\ 2 x & =3 y+4 \\ x & =\frac{3 y+4}{2} \ldots (1) \end{aligned} $$
$$ \begin{aligned} 9^x \times 27^y & =1 \\ 3^{2 x} \times 3^{3 y} & =3^0 \\ 3^{2 x+3 y} & =3^0 \\ 2 x+3 y & =0 … (2) \end{aligned} $$
$$ \begin{aligned} &\text { Gantikan (1) ke dalam (2), }\\ &\begin{aligned} 2\left(\frac{3 y+4}{2}\right)+3 y & =0 \\ 3 y+4+3 y & =0 \\ 6 y & =-4 \\ y & =-\frac{2}{3} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Gantikan } y=-\frac{2}{3} \text { ke dalam (1), }\\ &\begin{aligned} x & =\frac{3\left(-\frac{2}{3}\right)+4}{2} \\ & =\frac{-2+4}{2} \\ & =\frac{2}{2} \\ & =1 \end{aligned} \end{aligned} $$
Selesaikan persamaan serentak berikut.
$$ \text { (a) } 81^{(x+1)} \times 9^x=3^5 \operatorname{dan} 8^{2 x} \times 4\left(2^{2 y}\right)=128 $$
$$ \text { (b) } 4\left(4^x\right)=8^{y+2} \text { dan } 9^x \times 27^y=1 $$
Penyelesaian:
(a)
$$ \begin{aligned} 81^{(x+1)} \times 9^x & =3^5 \\ 3^{4(x+1)} \times 3^{2 x} & =3^5 \\ 3^{4 x+4} \times 3^{2 x} & =3^5 \\ 3^{4 x+2 x+4} & =3^5 \\ 6 x+4 & =5 \\ 6 x & =5-4 \\ 6 x & =1 \\ x & =\frac{1}{6} …(1) \end{aligned} $$
$$ \begin{aligned} 8^{2 x} \times 4\left(2^{2 y}\right) & =128 \\ \left(2^3\right)^{2 x} \times\left(2^2\right)\left(2^{2 y}\right) & =2^7 \\ 2^{6 x} \times 2^{2+2 y} & =2^7 \\ 2^{6 x+2+2 y} & =2^7 \\ 6 x+2+2 y & =7 \\ 6 x+2 y & =5 …(2) \end{aligned} $$
$$ \begin{aligned} &\text { Gantikan (1) ke dalam (2), }\\ &\begin{aligned} 6\left(\frac{1}{6}\right)+2 y & =5 \\ 1+2 y & =5 \\ 2 y & =5-1 \\ 2 y & =4 \\ y & =\frac{4}{2} \\ y & =2 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} 4\left(4^x\right) & =8^{y+2} \\ 2^2\left(2^{2 x}\right) & =2^{3(y+2)} \\ 2^{2+2 x} & =2^{3 y+6} \\ 2+2 x & =3 y+6 \\ 2 x & =3 y+4 \\ x & =\frac{3 y+4}{2} \ldots (1) \end{aligned} $$
$$ \begin{aligned} 9^x \times 27^y & =1 \\ 3^{2 x} \times 3^{3 y} & =3^0 \\ 3^{2 x+3 y} & =3^0 \\ 2 x+3 y & =0 … (2) \end{aligned} $$
$$ \begin{aligned} &\text { Gantikan (1) ke dalam (2), }\\ &\begin{aligned} 2\left(\frac{3 y+4}{2}\right)+3 y & =0 \\ 3 y+4+3 y & =0 \\ 6 y & =-4 \\ y & =-\frac{2}{3} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Gantikan } y=-\frac{2}{3} \text { ke dalam (1), }\\ &\begin{aligned} x & =\frac{3\left(-\frac{2}{3}\right)+4}{2} \\ & =\frac{-2+4}{2} \\ & =\frac{2}{2} \\ & =1 \end{aligned} \end{aligned} $$