Permudahkan setiap yang berikut.
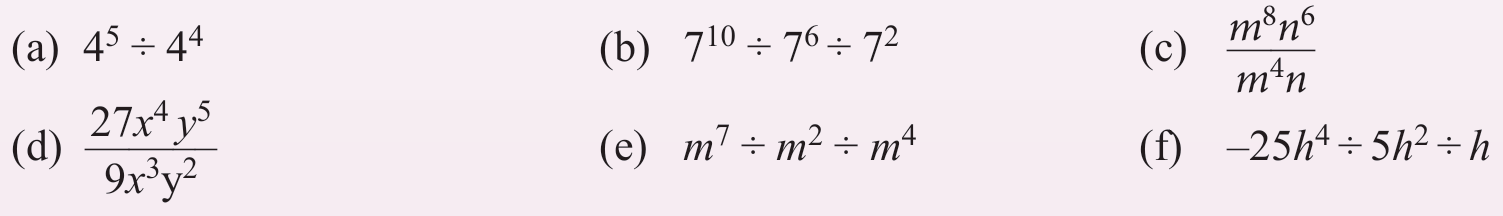
Penyelesaian:
(a)
$$
\begin{aligned}
& 4^5 \div 4^4 \\
& =4^{5-4} \\
& =4^1 \\
& =4
\end{aligned}
$$
(b)
$$
\begin{aligned}
& 7^{10} \div 7^6 \div 7^2 \\
& =7^{10-6} \div 7^2 \\
& =7^{4-2} \\
& =7^2
\end{aligned}
$$
(c)
$$
\begin{aligned}
& \frac{m^8 n^6}{m^4 n} \\
& =\left(m^8 \div m^4\right) \times\left(n^6 \div n\right) \\
& =m^{8-4} \times n^{6-1} \\
& =m^4 n^5
\end{aligned}
$$
(d)
$$
\begin{aligned}
& \frac{27 x^4 y^5}{9 x^3 y^2} \\
& =\frac{27}{9}\left(x^4 \div x^3\right)\left(y^5 \div y^2\right) \\
& =3\left(x^{4-3} \times y^{5-2}\right) \\
& =3 x y^3
\end{aligned}
$$
(e)
$$
\begin{aligned}
& m^7 \div m^2 \div m^4 \\
& =\left(m^{7-2}\right) \div m^4 \\
& =m^5 \div m^4 \\
& =m^{5-4} \\
& =m^1 \\
& =m
\end{aligned}
$$
(f)
$$
\begin{aligned}
& -25 h^4 \div 5 h^2 \div h \\
& =(-25 \div 5)\left(h^4 \div h^2 \div h\right) \\
& =-5\left(h^{4-2}\right) \div h \\
& =-5 h^2 \div h \\
& =-5\left(h^{2-1}\right) \\
& =-5 h^1 \\
& =-5 h
\end{aligned}
$$
Salin dan lengkapkan setiap persamaan di bawah.

Penyelesaian:
(a)

(b)

(c)

(d)

$$
\text { Jika } \frac{2^x \times 3^y}{2^4 \times 3^2}=6 \text {, tentukan nilai } x+y \text {. }
$$
Penyelesaian:
$$
\begin{aligned}
\frac{2^x \times 3^y}{2^4 \times 3^2} & =6 \\
\left(2^x \div 2^4\right) \times\left(3^y \div 3^2\right) & =2 \times 3 \\
2^{x-4} \times 3^{y-2} & =2^1 \times 3^1
\end{aligned}
$$
$$
\begin{aligned}
&\text { Bandingkan indeks bagi asas yang sama di kedua-dua belah }\\
&\begin{aligned}
x-4 & =1 \\
x & =1+4 \\
x & =5
\end{aligned}\\
&\begin{aligned}
y-2 & =1 \\
y & =1+2 \\
& =3
\end{aligned}\\
&\begin{aligned}
x+y & =5+3 \\
& =8
\end{aligned}
\end{aligned}
$$