1.1 Indeks - Matematik Tingkatan 1, 2 dan 3

1.1 Indeks

1.1.1 Indeks

1. Suatu nombor aⁿ bermakna nombor itu mempunyai n faktor yang sama bagi nombor a, untuk didarabkan sekali.

2. aⁿ dibaca ‘a kuasa n’ di mana a ialah asas dan n ialah indeks.

Contoh:

3. Jika a ialah suatu nombor bulat dan n ialah suatu integer positif, maka

4. Nilai suatu nombor yang ditulis dalam bentuk indeks boleh ditentukan dengan cara pendaraban berulang.

Contoh:

6⁴= 6 × 6 × 6 × 6

= 1296

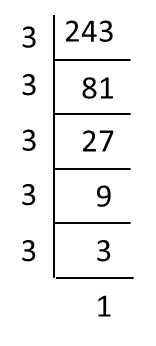
5. Suatu nombor boleh ditulis dalam tatatanda indeks dengan cara pembahagian berulang dengan nombor asas sehingga hasil bahagi menjadi 1.

Contoh:

243 = 3 × 3 × 3 × 3 × 3

= 3⁵

1.1.2 Pendaraban Nombor Kuasa

Pendaraban nombor dalam tatatanda indeks dengan asas yang sama boleh dipermudahkan dengan cara penambahan indeks.

a^m× aⁿ= a^m^{+ n}

Contoh:

3³× 3⁸= 3³⁺⁸

= 3¹¹

1.1.3 Pembahagian Melibatkan Tatatanda Indeks

1. Pembahagian dua nombor dalam tatatanda indeks dengan asas yang sama boleh dipermudahkan dengan cara penolakan indeks:

a^m÷ aⁿ= a^m^{- n}

Contoh:

4¹²÷ 4¹²= 4^12-12

= 4⁰

= 1

2. a⁰= 1

1.1.4 Kuasakan Nombor dan Sebutan Algebra Dalam Tatatanda Indeks kepada Suatu Kuasa

Suatu nombor kuasa yang dikuasakan boleh dipermudahkan dengan pendaraban indeks.

(a^m)ⁿ= (aⁿ)^m= a^mⁿ

Contoh:

(4³)⁷ = 4³×⁷

= 4²¹

1.1.5 Indeks Negatif

a^{- n} = \frac{1}{a^{n}}

Contoh:

5^{- 2} = \frac{1}{5^{2}} = \frac{1}{25}

1.1.6 Indeks Pecahan

a^{\frac{m}{n}} = \sqrt[n]{a^{m}} atau {(\sqrt[n]{a})}^{m}

Contoh:

\begin{array}{l} 64^{\frac{2}{3}} = \sqrt[3]{64^{2}} atau {(\sqrt[3]{64})}^{2} \\ = 16 \end{array}