Soalan 1:
Nyatakan setiap sebutan berikut dalam bentuk indeks positif.
(g)
$$
3 n^{-4}=3\left(\frac{1}{n^4}\right)=\frac{3}{n^4}
$$
(h)
$$
-5 n^{-6}=-5\left(\frac{1}{n^6}\right)=-\frac{5}{n^6}
$$
(i)
$$
\frac{2}{7} m^{-5}=\frac{2}{7}\left(\frac{1}{m^5}\right)=\frac{2}{7 m^5}
$$
(j)
$$
\left(-\frac{3}{8}\right) m^{-4}=\left(-\frac{3}{8}\right)\left(\frac{1}{m^4}\right)=-\frac{3}{8 m^4}
$$
(k)
$$
\left(\frac{2}{5}\right)^{-12}=\left(\frac{5}{2}\right)^{12}
$$
(l)
$$
\left(-\frac{3}{7}\right)^{-14}=\left(-\frac{7}{3}\right)^{14}
$$
(m)
$$
\left(\frac{x}{y}\right)^{-10}=\left(\frac{y}{x}\right)^{10}
$$
(n)
$$
\left(\frac{2 x}{3 y}\right)^{-4}=\left(\frac{3 y}{2 x}\right)^4
$$
(o)
$$
\left(\frac{1}{2 x}\right)^{-5}=(2 x)^5
$$
Nyatakan setiap sebutan berikut dalam bentuk indeks positif.
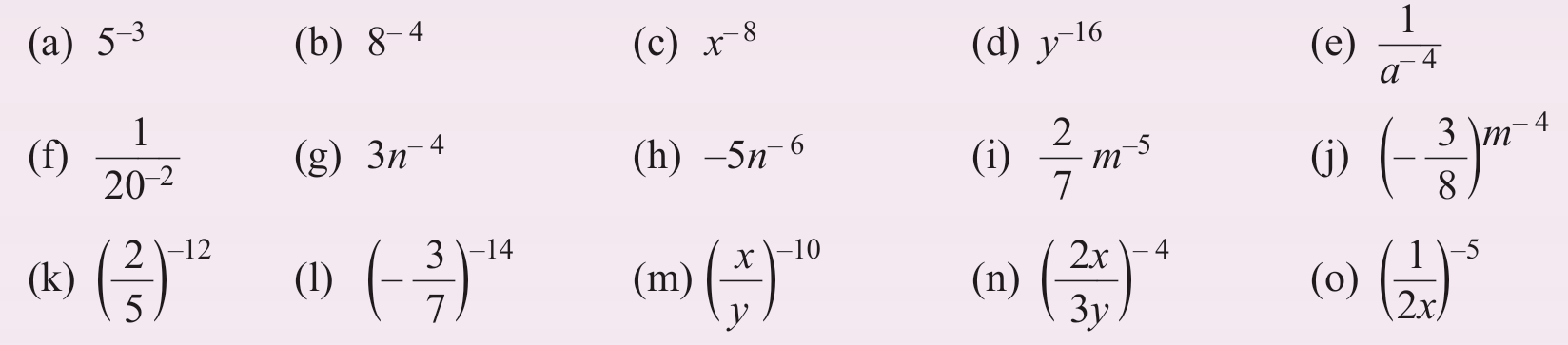
Penyelesaian:
(a)
$$
5^{-3}=\frac{1}{5^3}
$$
(b)
$$
8^{-4}=\frac{1}{8^4}
$$
(c)
$$
x^{-8}=\frac{1}{x^8}
$$
(d)
$$
y^{-16}=\frac{1}{y^{16}}
$$
(e)
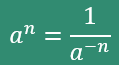
$$
\frac{1}{a^{-4}}=a^4
$$
(f)
$$
\frac{1}{20^{-2}}=20^2
$$
(g)
$$
3 n^{-4}=3\left(\frac{1}{n^4}\right)=\frac{3}{n^4}
$$
(h)
$$
-5 n^{-6}=-5\left(\frac{1}{n^6}\right)=-\frac{5}{n^6}
$$
(i)
$$
\frac{2}{7} m^{-5}=\frac{2}{7}\left(\frac{1}{m^5}\right)=\frac{2}{7 m^5}
$$
(j)
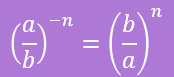
$$
\left(-\frac{3}{8}\right) m^{-4}=\left(-\frac{3}{8}\right)\left(\frac{1}{m^4}\right)=-\frac{3}{8 m^4}
$$
(k)
$$
\left(\frac{2}{5}\right)^{-12}=\left(\frac{5}{2}\right)^{12}
$$
(l)
$$
\left(-\frac{3}{7}\right)^{-14}=\left(-\frac{7}{3}\right)^{14}
$$
(m)
$$
\left(\frac{x}{y}\right)^{-10}=\left(\frac{y}{x}\right)^{10}
$$
(n)
$$
\left(\frac{2 x}{3 y}\right)^{-4}=\left(\frac{3 y}{2 x}\right)^4
$$
(o)
$$
\left(\frac{1}{2 x}\right)^{-5}=(2 x)^5
$$
Soalan 2:
Nyatakan setiap sebutan berikut dalam bentuk indeks negatif.
(d)
$$
\frac{1}{n^9}=n^{-9}
$$
(e)
$$
10^2=\frac{1}{10^{-2}}
$$
(f)
$$
(-4)^3=\frac{1}{(-4)^{-3}}
$$
(g)
$$
m^{12}=\frac{1}{m^{-12}}
$$
(h)
$$
n^{16}=\frac{1}{n^{-16}}
$$
(i)
$$
\left(\frac{4}{7}\right)^9=\left(\frac{7}{4}\right)^{-9}
$$
(j)
$$
\left(\frac{x}{y}\right)^{10}=\left(\frac{y}{x}\right)^{-10}
$$
Nyatakan setiap sebutan berikut dalam bentuk indeks negatif.
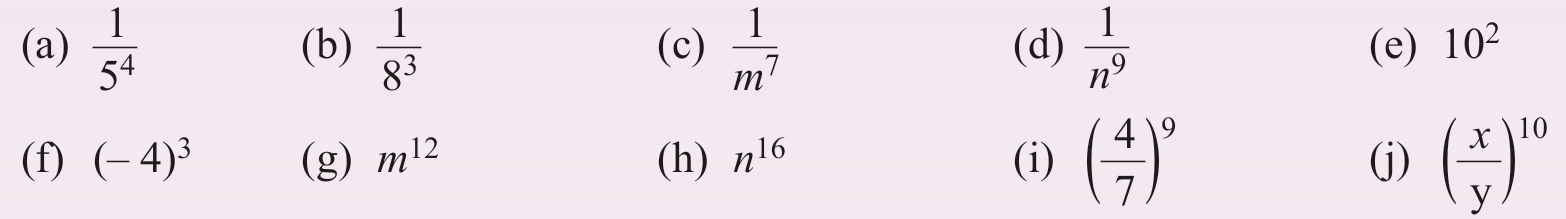
Penyelesaian:
(a)
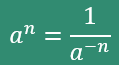
$$
\frac{1}{5^4}=5^{-4}
$$
(b)
$$
\frac{1}{8^3}=8^{-3}
$$
(c)
$$
\frac{1}{m^7}=m^{-7}
$$
(d)
$$
\frac{1}{n^9}=n^{-9}
$$
(e)
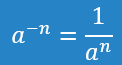
$$
10^2=\frac{1}{10^{-2}}
$$
(f)
$$
(-4)^3=\frac{1}{(-4)^{-3}}
$$
(g)
$$
m^{12}=\frac{1}{m^{-12}}
$$
(h)
$$
n^{16}=\frac{1}{n^{-16}}
$$
(i)
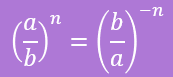
$$
\left(\frac{4}{7}\right)^9=\left(\frac{7}{4}\right)^{-9}
$$
(j)
$$
\left(\frac{x}{y}\right)^{10}=\left(\frac{y}{x}\right)^{-10}
$$
Soalan 3:
Permudahkan setiap yang berikut.
(b)
$$
\begin{aligned}
& \frac{\left(2^3 \times 3^2\right)^3}{\left(2 \times 3^4\right)^5} \\
& =\frac{2^{3 \times 3} \times 3^{2 \times 3}}{2^{1 \times 5} \times 3^{4 \times 5}} \\
& =\frac{2^9 \times 3^6}{2^5 \times 3^{20}} \\
& =2^{9-5} \times 3^{6-20} \\
& =2^4 \times 3^{-14} \\
& =2^4 \times \frac{1}{3^{14}} \\
& =\frac{2^4}{3^{14}}
\end{aligned}
$$
(c)
$$
\begin{aligned}
& \frac{\left(5^2\right)^5}{\left(2^3\right)^{-2} \times\left(5^4\right)^2} \\
& =\frac{5^{2 \times 5}}{2^{3 \times-2} \times 5^{4 \times 2}} \\
& =\frac{5^{10}}{2^{-6} \times 5^8} \\
& =\frac{5^{10-8}}{2^{-6}} \\
& =5^2 \times \frac{1}{2^{-6}} \\
& =5^2 \times 2^6 \\
& =2^6 \times 5^2
\end{aligned}
$$
(d)
$$
\begin{aligned}
& \frac{3 m^2 n^4 \times\left(m n^3\right)^{-2}}{9 m^3 n^5} \\
& =\frac{3 m^2 n^4 \times m^{1 \times-2} n^{3 \times-2}}{9 m^3 n^5} \\
& =\frac{3 m^2 n^4 \times m^{-2} n^{-6}}{9 m^3 n^5} \\
& =\frac{3}{9} \times m^{2+(-2)-3} \times n^{4+(-6)-5} \\
& =\frac{1}{3} \times m^{-3} n^{-7} \\
& =\frac{1}{3} \times \frac{1}{m^3} \times \frac{1}{n^7} \\
& =\frac{1}{3 m^3 n^7}
\end{aligned}
$$
(e)
$$
\begin{aligned}
\frac{\left(2 m^2 n^2\right)^{-3} \times\left(3 m n^2\right)^4}{\left(9 m^3 n\right)^2} & =\frac{2^{-3} m^{-6} n^{-6} \times 3^4 m^4 n^8}{9^2 m^6 n^2} \\
& =\frac{2^{-3} \times 3^4}{9^2} \times m^{-6+4-6} \times n^{-6+8-2} \\
& =\frac{3^4}{9^2 \times 2^3} \times m^{-8} \times n^0 \\
& =\frac{3^4}{\left(3^2\right)^2 \times 2^3} \times \frac{1}{m^8} \quad n^0=1 \\
& =\frac{3^4}{3^4 \times 2^3} \times \frac{1}{m^8} \\
& =3^{4-4} \times \frac{1}{2^3} \times \frac{1}{m^8} \\
& =3^0 \times \frac{1}{2^3} \times \frac{1}{m^8} \\
& =\frac{1}{8 m^8}
\end{aligned}
$$
(f)
$$
\begin{aligned}
\frac{\left(4 m^2 n^4\right)^2}{\left(2 m^{-2} n\right)^5 \times\left(3 m^4 n\right)^2} & =\frac{4^2 m^4 n^8}{2^5 m^{-10} n^5 \times 3^2 m^8 n^2} \\
& =\frac{4^2}{2^5 \times 3^2} \times m^{4-(-10)-8} \times n^{8-5-2} \\
& =\frac{2^{4-5}}{3^2} \times m^6 \times n^1 \\
& =\frac{2^{-1}}{3^2} \times m^6 \times n \\
& =\frac{1}{2 \times 9} m^6 n \\
& =\frac{1}{18} m^6 n \\
& =\frac{m^6 n}{18}
\end{aligned}
$$
Permudahkan setiap yang berikut.
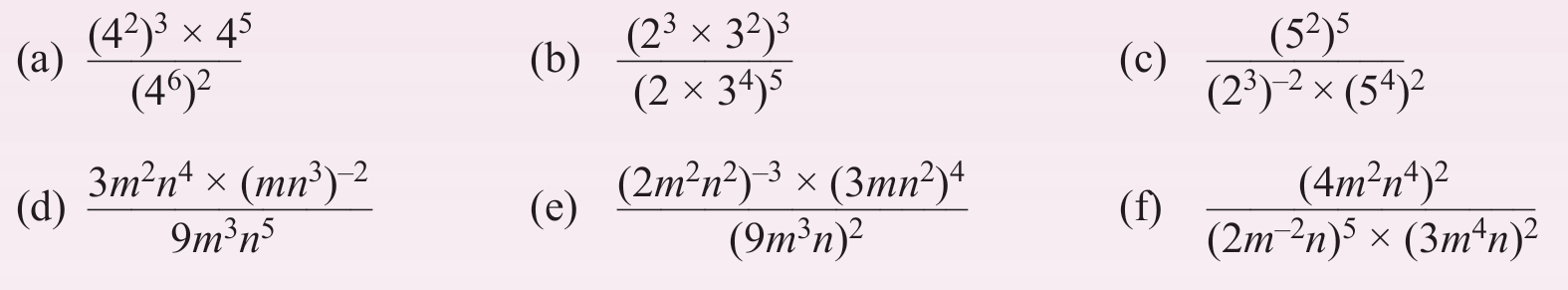
Penyelesaian:
(a)
$$
\begin{aligned}
& \frac{\left(4^2\right)^3 \times 4^5}{\left(4^6\right)^2} \\
& =\frac{4^{2 \times 3} \times 4^5}{4^{6 \times 2}} \\
& =\frac{4^6 \times 4^5}{4^{12}} \\
& =4^{6+5-12} \\
& =4^{-1} \\
& =\frac{1}{4}
\end{aligned}
$$
(b)
$$
\begin{aligned}
& \frac{\left(2^3 \times 3^2\right)^3}{\left(2 \times 3^4\right)^5} \\
& =\frac{2^{3 \times 3} \times 3^{2 \times 3}}{2^{1 \times 5} \times 3^{4 \times 5}} \\
& =\frac{2^9 \times 3^6}{2^5 \times 3^{20}} \\
& =2^{9-5} \times 3^{6-20} \\
& =2^4 \times 3^{-14} \\
& =2^4 \times \frac{1}{3^{14}} \\
& =\frac{2^4}{3^{14}}
\end{aligned}
$$
(c)
$$
\begin{aligned}
& \frac{\left(5^2\right)^5}{\left(2^3\right)^{-2} \times\left(5^4\right)^2} \\
& =\frac{5^{2 \times 5}}{2^{3 \times-2} \times 5^{4 \times 2}} \\
& =\frac{5^{10}}{2^{-6} \times 5^8} \\
& =\frac{5^{10-8}}{2^{-6}} \\
& =5^2 \times \frac{1}{2^{-6}} \\
& =5^2 \times 2^6 \\
& =2^6 \times 5^2
\end{aligned}
$$
(d)
$$
\begin{aligned}
& \frac{3 m^2 n^4 \times\left(m n^3\right)^{-2}}{9 m^3 n^5} \\
& =\frac{3 m^2 n^4 \times m^{1 \times-2} n^{3 \times-2}}{9 m^3 n^5} \\
& =\frac{3 m^2 n^4 \times m^{-2} n^{-6}}{9 m^3 n^5} \\
& =\frac{3}{9} \times m^{2+(-2)-3} \times n^{4+(-6)-5} \\
& =\frac{1}{3} \times m^{-3} n^{-7} \\
& =\frac{1}{3} \times \frac{1}{m^3} \times \frac{1}{n^7} \\
& =\frac{1}{3 m^3 n^7}
\end{aligned}
$$
(e)
$$
\begin{aligned}
\frac{\left(2 m^2 n^2\right)^{-3} \times\left(3 m n^2\right)^4}{\left(9 m^3 n\right)^2} & =\frac{2^{-3} m^{-6} n^{-6} \times 3^4 m^4 n^8}{9^2 m^6 n^2} \\
& =\frac{2^{-3} \times 3^4}{9^2} \times m^{-6+4-6} \times n^{-6+8-2} \\
& =\frac{3^4}{9^2 \times 2^3} \times m^{-8} \times n^0 \\
& =\frac{3^4}{\left(3^2\right)^2 \times 2^3} \times \frac{1}{m^8} \quad n^0=1 \\
& =\frac{3^4}{3^4 \times 2^3} \times \frac{1}{m^8} \\
& =3^{4-4} \times \frac{1}{2^3} \times \frac{1}{m^8} \\
& =3^0 \times \frac{1}{2^3} \times \frac{1}{m^8} \\
& =\frac{1}{8 m^8}
\end{aligned}
$$
(f)
$$
\begin{aligned}
\frac{\left(4 m^2 n^4\right)^2}{\left(2 m^{-2} n\right)^5 \times\left(3 m^4 n\right)^2} & =\frac{4^2 m^4 n^8}{2^5 m^{-10} n^5 \times 3^2 m^8 n^2} \\
& =\frac{4^2}{2^5 \times 3^2} \times m^{4-(-10)-8} \times n^{8-5-2} \\
& =\frac{2^{4-5}}{3^2} \times m^6 \times n^1 \\
& =\frac{2^{-1}}{3^2} \times m^6 \times n \\
& =\frac{1}{2 \times 9} m^6 n \\
& =\frac{1}{18} m^6 n \\
& =\frac{m^6 n}{18}
\end{aligned}
$$